Interactive graphs/plots help visualize and better understand the functionsG(x) " • The derivative of a difference is the difference of the derivatives Example 6 Find an equation for the tangent line to the graph of k(x)=4x3 −7x2 at x =1Derivative Here, n = 4 d/dx x(n) = nx n1 = d/dx (x

5 Derivative Of The Logarithmic Function
Differentiate the function. y = 6x2 + 8x + 8 x
Differentiate the function. y = 6x2 + 8x + 8 x-Function Derivative y = a·xn dy dx = a·n·xn−1 Power Rule y = a·un dy dx = a·n·un−1 du dx PowerChain Rule Ex1a Find the derivative of y = 8(6x21)8 Answer y0 = 384(6x 21)7 a = 8, n = 8 u = 6x21 ⇒ du dx = 6 ⇒ y0 = 8·8·(6x21)7 ·6 Ex1b Find the derivative of y = 8 4x2 7x28 4 Answer y0 = 32(8x 7) 4x2 7x 28 3 a 8 Differentiation of Implicit Functions by M Bourne We meet many equations where y is not expressed explicitly in terms of x only, such as f(x, y) = y 4 2x 2 y 2 6x 2 = 7 You can see several examples of such expressions in the Polar Graphs section It is usually difficult, if not impossible, to solve for y so that we can then find `(dy)/(dx)` We need to be able to find



14 5 The Chain Rule For Multivariable Functions Mathematics Libretexts
Answer to Differentiate the functiony = ln(e−x xe−x) Calculus Early Transcendentals (5th Edition) Edit edition Problem 17E from Chapter 38 Differentiate the functiony = ln(e−x xe−x)Find the derivative of f(x) = x2 We use a variety of different notations to express the derivative of a function In Example 312 we showed that if f(x) = x2 − 2x, then f ′ (x) = 2x − 2 If we had expressed this function in the form y = x2 − 2x, we could have expressed the derivative as y ′Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
Derivative of arctanx at x=0;The second part of the function is plus square X times one minus zero And we also used the power all to get that And if we simplify this yoon further, we have d Y The ex is equal to one over to route X Times X minus one Close the square root of X and that is your final answer"} Ex 55, 8 Differentiate the functions in, 〖(sin𝑥)〗^𝑥 sin^(−1) √𝑥 Let 𝑦=(sin𝑥 )^𝑥 sin^(−1)√𝑥 Let 𝑢 = (sin𝑥 )^𝑥 & 𝑣 = sin^(−1)√𝑥 𝑦 = 𝑢 𝑣 Differentiating both sides 𝑤𝑟𝑡𝑥 𝑑𝑦/𝑑𝑥
F(x) " − d dx!10) y = (2x2 − 5)3 x2 − 2 dy dx = y(12 x 2x2 − 5 x x2 − 2) = x(2x2 − 5)2(14 x2 − 29) x2 − 2 Use logarithmic differentiation to differentiate each function with respect to x You do not need to simplify or substitute for y 11) y = (5x − 4)4 (3x2 5)5 ⋅ (5x4 − 3)3 dy dx = y( 5x − 4 − 30 x 3x2 5 − 60 x3 5x4 − 3Y ' (1 / y) = ln x x (1 / x) = ln x 1 , where y ' = dy/dx Multiply both sides by y y ' = (ln x 1)y Substitute y by x x to obtain y ' = (ln x 1)x x Exercise Find the first derivative of y = xx 2 Answer to Above Exercise y ' = x x 3 (x ln x x 2) More on differentiation and derivatives



Differentiate The Function H T 9 Squareroot T Chegg Com




14 5 The Chain Rule For Multivariable Functions Mathematics Libretexts
There are two ways we can find the derivative of x^x It's important to notice that this function is neither a power function of the form x^k nor an exponential function of the form b^x, so we can't use the differentiation formulas for either of these cases directly (i) Let y=x^x, and take logarithms of both sides of this equation ln(y)=ln(x^x)Differentiate the function y = (x^2 4x 3)/sqrt(x)The derivative of `y = (sqrt x x)/x^2` has to be determined Now for the function `y = (sqrt x x)/x^2` divide each term of the numerator by the denominator x^2



Increasing And Decreasing Functions



3 7 Derivatives Of Inverse Functions Mathematics Libretexts
Created by T Madas Created by T Madas Question 3 Differentiate the following expressions with respect to x a) y x x= −2 64 2 24 5 dy x x dx = − b) 3 y x x= −5 63 2 1 dy 15 9x x2 2 dx = − The answer is x − 4 √x2 −8x y = √x(x −8) ⇒ y = √x2 − 8x ⇒ y' = 1 2√x2 − 8x ⋅ (2x −8) = 2(x − 4) 2√x2 −8x = x −4 √x2 − 8xThe derivative of a function is one of the basic concepts of mathematics Together with the integral, derivative occupies a central place in calculus The process of finding the derivative is called differentiationThe inverse operation for differentiation is called integration The derivative of a function at some point characterizes the rate of change of the function at this




3 Ways To Differentiate The Square Root Of X Wikihow



3 8 Implicit Differentiation Calculus Volume 1
Product rule u'v uv Quotient Rule "' Chain Rule Derivative of the inside function x Derivative of the outside function (See video for more formal definition) Differentiate the following functions 1 f(x) (4x 1)(6x 3) (x25x 7)(6x2 5x 4) 2 y 3 y (x21) (3x3 6x 5) 4(4x2 2x 1) 4 y 7 5 f(x)= 5x x1 6 f(x) 62x x24 24x3Derivative of a Constant lf c is any real number and if f(x) = c for all x, then f ' (x) = 0 for all x That is, the derivative of a constant function is the zero function It is easy to see this geometrically Referring to Figure 1, we see that the graph of the constant function f(x) = c is a horizontal lineDifferentiate the function y = e^(x1) 1



Http Www Apsva Us Wp Content Uploads Legacy Assets Washingtonlee 3163bc16 Derivative Graph Notes Pdf



5 Derivative Of The Logarithmic Function
Inverse Functions Implicit differentiation can help us solve inverse functions The general pattern is Start with the inverse equation in explicit form Example y = sin −1 (x) Rewrite it in noninverse mode Example x = sin (y) Differentiate this function with respect to xThe slope of a line like 2x is 2, or 3x is 3 etc; 2 Take the natural logarithm of both sides You need to manipulate the function to help find a standard derivative in terms of the variable x {\displaystyle x} This begins by taking the natural logarithm of both sides, as follows ln y = ln a x {\displaystyle \ln y=\ln a^ {x}} 3 Eliminate the exponent




Ex 5 5 2 Differentiate Root X 1 X 2 X 3 X 4 X 5




Worked Example Implicit Differentiation Video Khan Academy
This is called logarithmic differentiation It's easiest to see how this works in an example Example 1 Differentiate the function y = x5 (1−10x)√x2 2 y = x 5 ( 1 − 10 x) x 2 2 Show Solution Differentiating this function could be done with a product rule and a quotient rule However, that would be a fairly messy processDifferentiate (x^2 y)/(y^2 x) wrt x The derivative is an important tool in calculus that represents an infinitesimal change in a function with respect to one of its variables Given a function , there are many ways to denote the derivative of with respect toThe Derivative Calculator supports computing first, second, , fifth derivatives as well as differentiating functions with many variables (partial derivatives), implicit differentiation and calculating roots/zeros You can also check your answers!




Differentiate The Function Y A F X Choose The Chegg Com



What Is The Differentiation Of Y X 7 X 2 X 3 Quora
Implicit Differentiation Implicit and Explicit functions An explicit function is an function expressed as y = f(x) such as y = 2x 3 5 y is defined implicitly if both x and y occur on the same side of the equation such as x 2 y 2 = 4 we can think of y as function of x and write x 2 y(xExamples Inverse functions A common type of implicit function is an inverse functionNot all functions have a unique inverse function If g is a function of x that has a unique inverse, then the inverse function of g, called g −1, is the unique function giving a solution of the equation = for x in terms of yThis solution can then be written asAnswer to Evaluate the derivative of the following function at the given point 18{x^3}{y^2} 6{y^3} = 8;




Differentiate The Following Function Part 1 Of 3 The Chegg Com




Derivative Of F X 1 X Using The Limit Definition Youtube
C f' (x)=−2xcos(x2) D f' (x)=2xcos(x) E f' (x)=2xsin(x2) Question 8 Find the derivative of the exponential function, y=esec3θ A y'=esec(3θ) tan (3θ) B y'=3esec(3θ) tan (3θ) C y'=sec(3θ) tan (3θ) D y'=3esec3θ ∗sec(3θ) tan(3θ) E y'=3esec(3θ) Question 9 Let f and g be inverse functions The following table lists a few values of f ,g, and f 'Differentiate the function {eq}y = e^{x 2} 8 {/eq} Differentiating a function The given function is in the form, {eq}f(x) = e^{x c} c {/eq}, where {eq}c {/eq} is a constant= f!(x)−g!(x) • d dx!
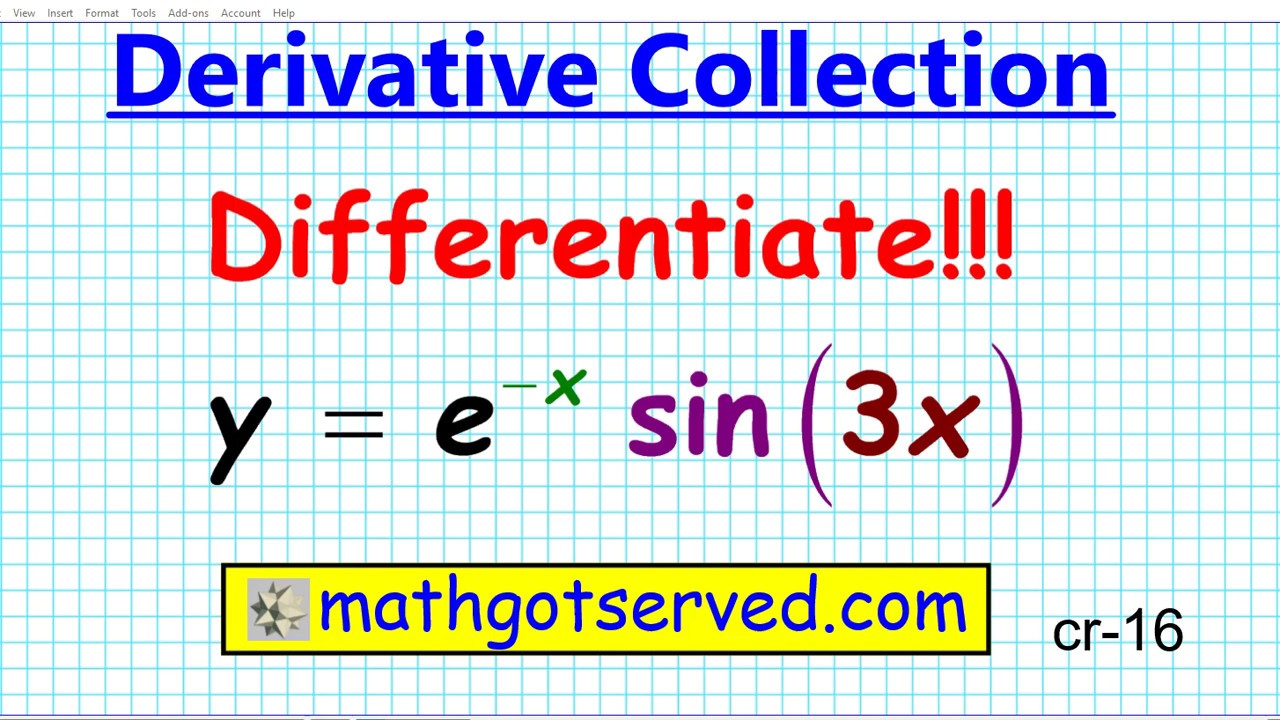



How To Find The Differentiate E X Sin 3x Chain Rule Derivative Collection Ap Calc Calculus Cr 16 Youtube



5 Derivative Of The Logarithmic Function
Textbook solution for Essential Calculus Early Transcendentals 2nd Edition James Stewart Chapter 33 Problem 22E We have stepbystep solutions for your textbooks written by Bartleby experts!Differentiate the functiony = log2(e−x cos πx) Get solutions We have solutions for your book!Make use of this free online derivative calculator to differentiate a function You can use this derivative calculator to convert functions from one form to another Example What is the derivative of x 4?
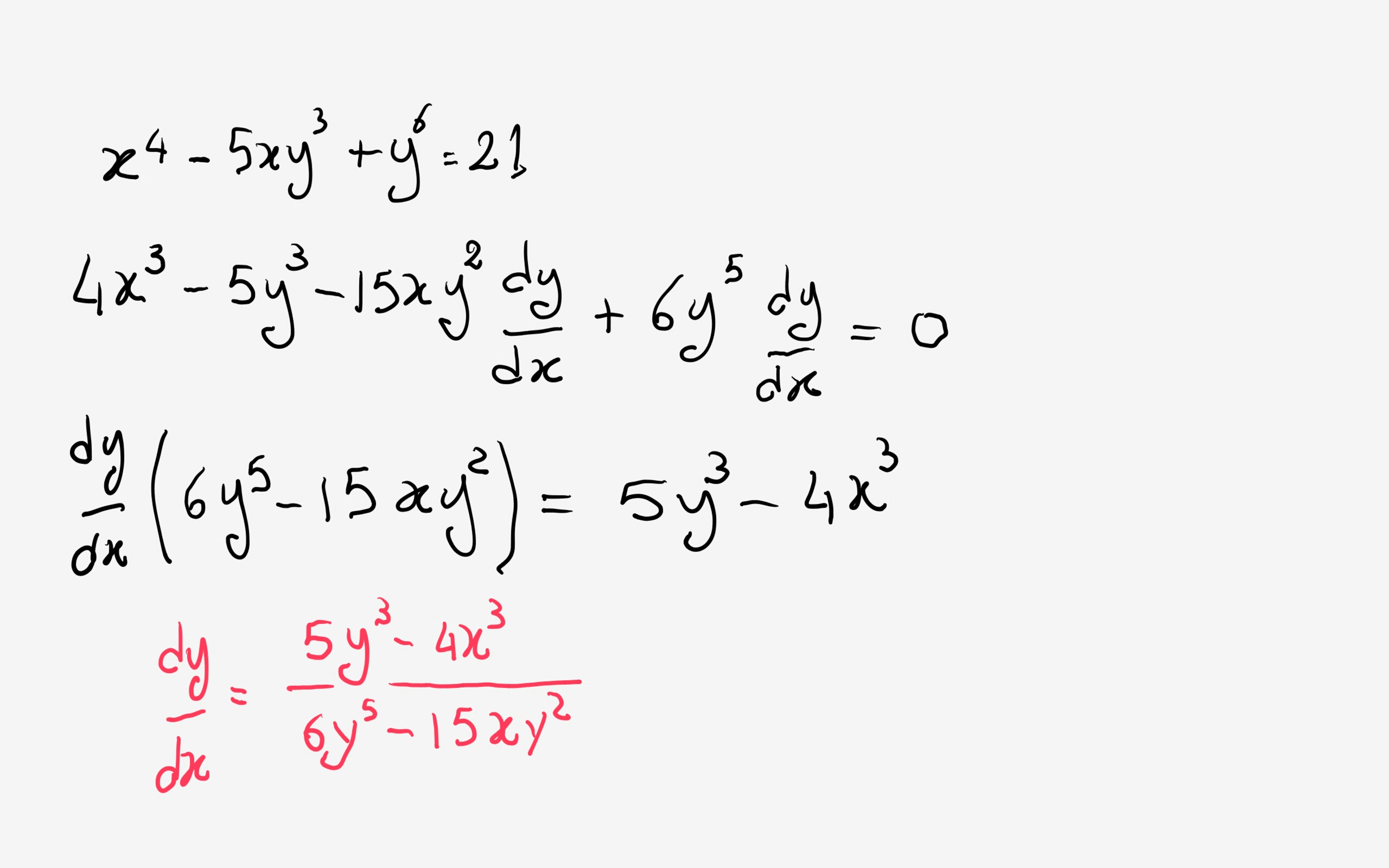



How Do You Find The Implicit Differentiation Of X 4 5xy 3 Y 6 21 Socratic




Differentiate The Function Y Ex 5 9 Y Chegg Com
10Answers #1 0 Find the derivative of the following via implicit differentiation d/dx (y) = d/dx ( (x sqrt (36x^2))36 sin^ (1) (x/6)) The derivative of y is y' (x) y' (x) = d/dx ( (x sqrt (36x^2))36 sin^ (1) (x/6)) Differentiate the sum term by term and factor out constants Ex 55, 7 Differentiate the functions in, 〖(log〖𝑥)〗〗^𝑥 𝑥^log𝑥 Let 𝑦 = 〖(log〖𝑥)〗〗^𝑥 𝑥^log𝑥 Let 𝑢 = 〖(log〖𝑥)〗〗^𝑥 , 𝑣 = 𝑥^log𝑥 𝑦 = 𝑢𝑣 Differentiating both sides 𝑤𝑟𝑡𝑥 𝑑𝑦/𝑑𝑥 = (𝑑 (𝑢 𝑣))/𝑑𝑥 𝑑𝑦/𝑑𝑥 = 𝑑𝑢/𝑑𝑥 𝑑𝑣/𝑑𝑥−2x4 5 8) y = (−x4 − 3)−2 1 ©F f2h0 21D34 0K muFt HaQ DSBo cf DtEw XaErXe2 BLRLYC7 c r TAkl rl 4 Ir xiog3h Dt1sc lr meAsOesr Jvse wdaV R MMtaOdJeL KwQiIt2hG DINnYfGiUn0igtve 6 XCta jl Qc3uwlfuxs 8 6 Worksheet by Kuta Software LLC



Curve Sketching




Differentiate The Following Function 9 R 7 0 5 Y Chegg Com
The Derivative tells us the slope of a function at any point There are rules we can follow to find many derivatives For example The slope of a constant value (like 3) is always 0;And so on Here are useful rules to help you work out the derivatives of many functions (with examples below)Note the little mark ' means derivative of, and All functions of type uv are defined with uv = evlnu Here √xx = e1 2xlnx y2 = xx Then upon differentiating 2yy ′ = (1 lnx)xx From which y ′ = 1 2y(1 lnx)xx (x ≠ 0) Giving y ′ = 1 2√xx(1 lnx)xx Thus y ′ = 1 2(1 lnx)√xx




Worked Example Chain Rule With Table Video Khan Academy



3 The Derivative From First Principles
SOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sidesThe difference rule Let f(x)andg(x) be differentiable functions • (f(x)−g(x))!\\quad (2, 3) By signing up, you'll get




What Is The Derivative Of Xy How To Steps Video Lesson Transcript Study Com




Implicit Differentiation
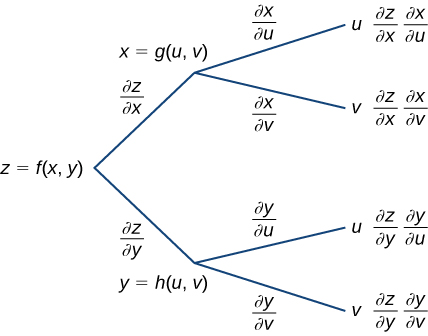
Functions can also depend on other functions For instance, suppose that f depends on both x and y, whilst x and y themselves depend on t Then you would enter f(x,y) x(t) y(t) in the functions text area, but refer to the functions simply as f, x and y within the expression itselfF(x)−g(x) " = d dx!Composite functions are functions of a function If we have y = f(t) and t = g(x), then the derivative of y with respect to x is, Example 1 Differentiate y = (3x –1) 2 with respect to x Let t = 3x – 1 y = t 2 dt dx = 3 dy dt = 2t Using the chain rule dx



Derivative Calculator With Steps



6 Derivative Of The Exponential Function
Calculus Find the Derivative d/dx y=8^x y = 8x y = 8 x Differentiate using the Exponential Rule which states that d dx ax d d x a x is axln(a) a x ln ( a) where a a = 8 8 8xln(8) 8 x ln ( 8)Finding the derivative of x x depends on knowledge of the natural log function and implicit differentiation Let y = x x If you take the natural log of both sides you get y = x x then ln (y) = ln (x x) = x ln (x) Now differentiate both sides with respect to x, recalling that y is a function of x 1 / y y' = ln (x) x 1 / x = ln (x) 1For example, the equation y − x 2 = 1 y − x 2 = 1 defines the function y = x 2 1 y = x 2 1 implicitly Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test)




Implicit Differentiation




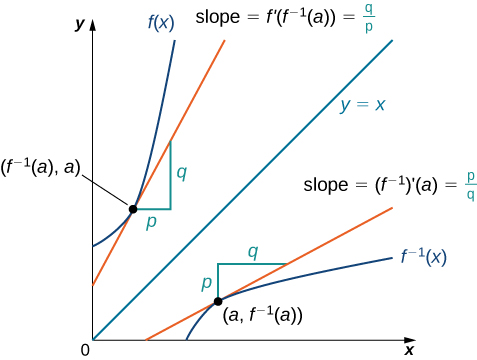
Derivatives Of Inverse Functions From Equation Video Khan Academy
Textbook solution for Calculus and Its Applications (11th Edition) 11th Edition Marvin L Bittinger Chapter 17 Problem 11E We have stepbystep solutions for your textbooks written by Logarithmic Differentiation Take the logarithm of both sides lny = ln(x8x) = 8xlnx Now differentiate implicitly 1 y dy dx = 8lnx 8x( 1 x) = 8lnx 8 dy dxFree derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graph




What Is The Differentiation Of Y X 7 X 2 X 3 Quora




5 Derivative Of The Logarithmic Function
Implicit Differentiation In most discussions of math, if the dependent variable is a function of the independent variable , we express in terms of If this is the case, we say that is an explicit function of For example, when we write the equation , we are defining explicitly in terms of On the other hand, if the relationship between the function and the variable is expressed by an equationA function of several real variables f R m → R n is said to be differentiable at a point x 0 if there exists a linear map J R m → R n such that → ‖ () () ‖ ‖ ‖ = If a function is differentiable at x 0, then all of the partial derivatives exist at x 0, and the linear map J is given by the Jacobian matrixA similar formulation of the higherdimensional derivative is provided byFind the Derivative d/dx y=x//x y = x 8 − 8 x y = x 8 8 x By the Sum Rule, the derivative of x 8 − 8 x x 8 8 x with respect to x x is d dx x 8 d dx− 8 x d d x x 8 d d x 8 x d dx x 8 d dx − 8 x d d x x 8 d d x 8 x Evaluate d dx x 8 d d x x 8 Tap for more steps
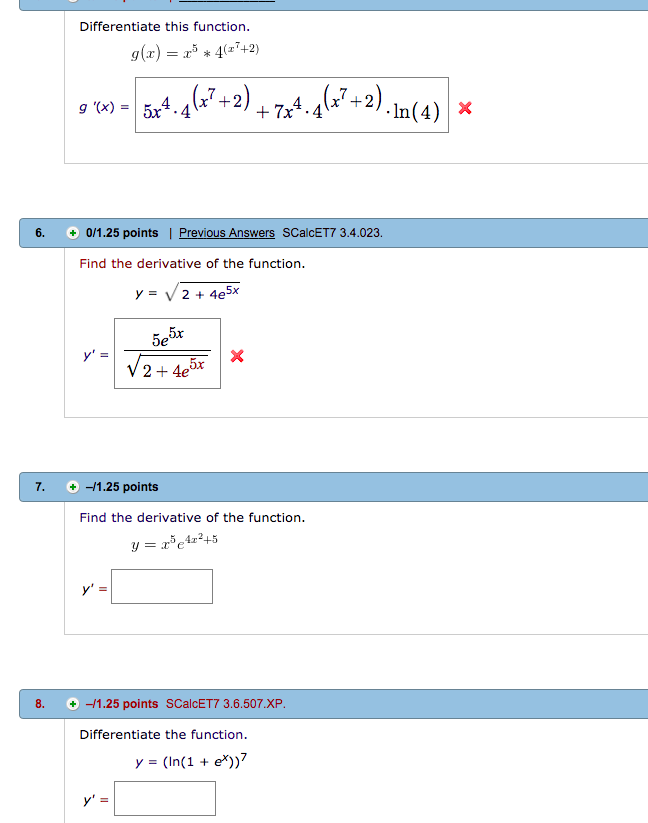



Differentiate This Function G Z 2 5 4042 Chegg Com



What Is The Derivative Of 1 X Quora
Chapter Problem FS show all show all steps Differentiate the function y = log 2 (e −x cos πx) Stepbystep solution 100 %(4 ratings) for this solution Chapter Problem FS show all show




Derivative Calculator Wolfram Alpha
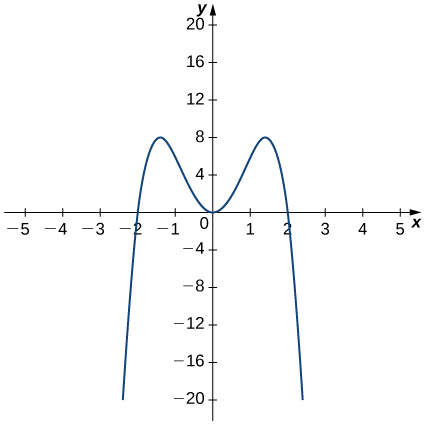



3 2 The Derivative As A Function Calculus Volume 1
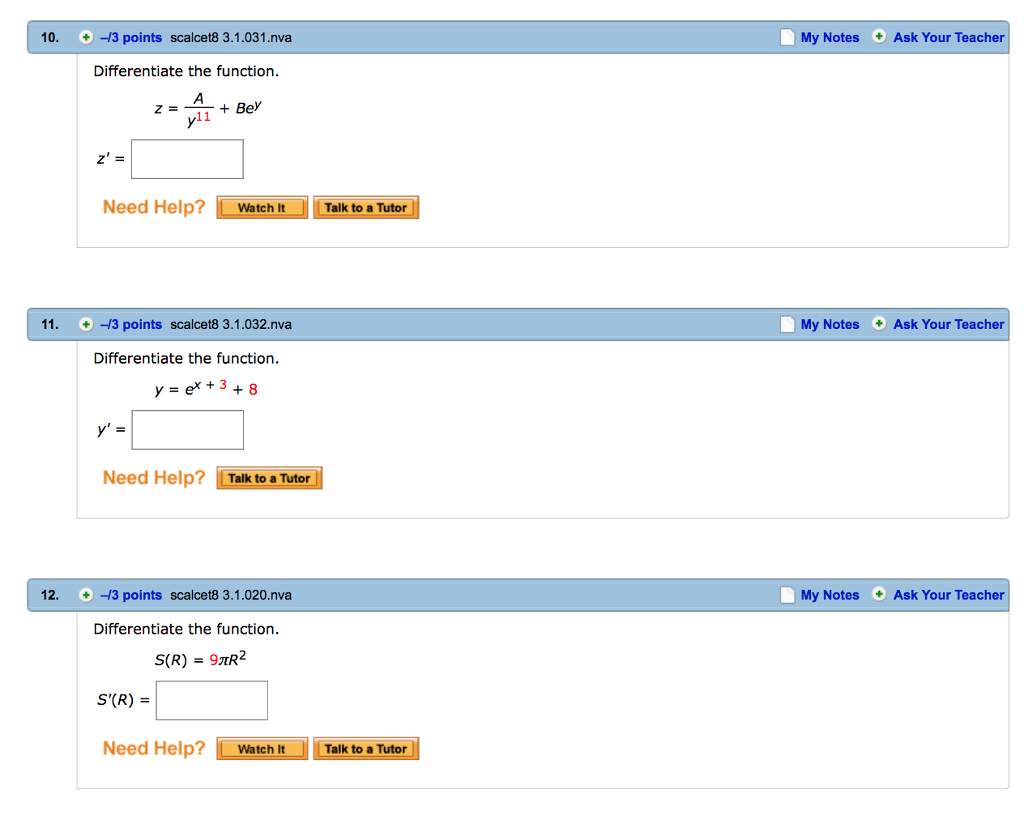



Differentiate The Function Z A Y 11 Be Y Z Chegg Com




3 Ways To Differentiate The Square Root Of X Wikihow




Find The Derivative Of Y Sqrt X 2 1



Implicit And Logarithmic Differentiation



3 The Derivative From First Principles



Automatic Differentiation Wikipedia



How Do You Determine Whether The Function F X Ln X 2 7 Is Concave Up Or Concave Down And Its Intervals Socratic




Derivative Wikipedia




Derivative Using The Definition Example 2 Youtube
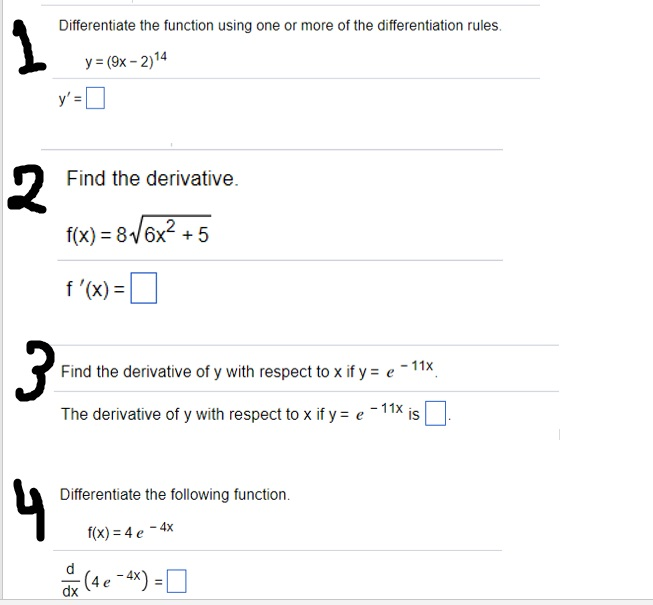



Differentiate The Function Using One Or More Of The Chegg Com




Y X Ln X Differentiate The Function Youtube




Ex 5 5 17 Differentiate Using Product Rule By Expanding Product



6 Derivative Of The Exponential Function
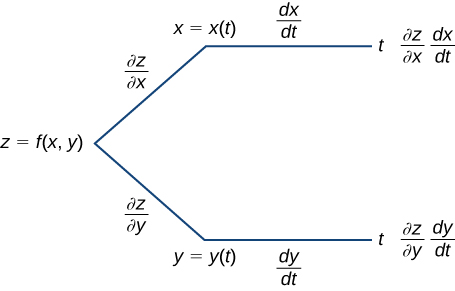



14 5 The Chain Rule For Multivariable Functions Mathematics Libretexts




Solutions To Implicit Differentiation Problems




8 10 Pointsscalcet8 3 1 032 Differentiate The Chegg Com



1




Derivative Rules



6 Derivative Of The Exponential Function
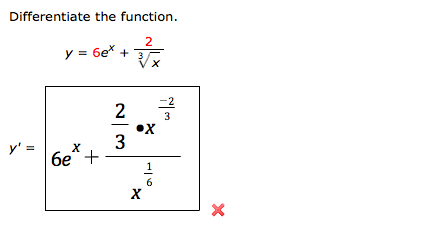



Differentiate The Function Y 6ex 2 3 X Chegg Com




Ex 5 5 3 Differentiate The Function Log X Cos X Teachoo



Derivatives Of Trigonometric Functions



The Fundamental Theorem Of Calculus




Find The Derivative Of The Following W R T X I 7x 8 4 5



Http Www Ed Ac Uk Files Atoms Files Week3 Answers Pdf



3 2 The Derivative As A Function Calculus Volume 1
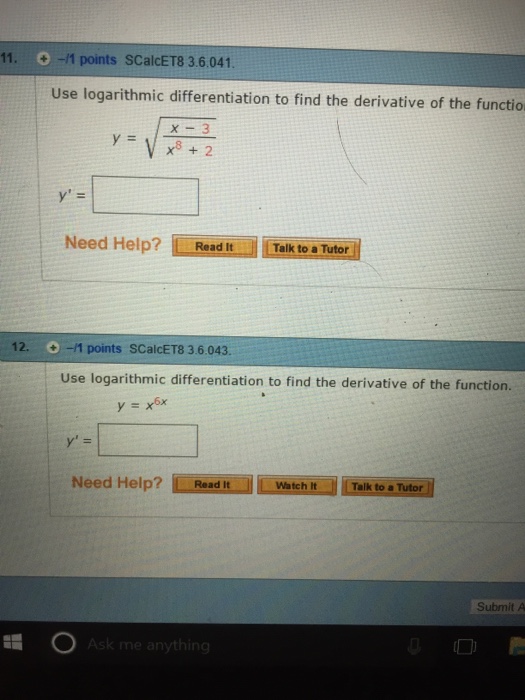



Use Logarithmic Differentiation To Find The Chegg Com




Suppose We Wanted To Differentiate The Function H Chegg Com




Differentiate The Function Y 8x 2 6x Chegg Com
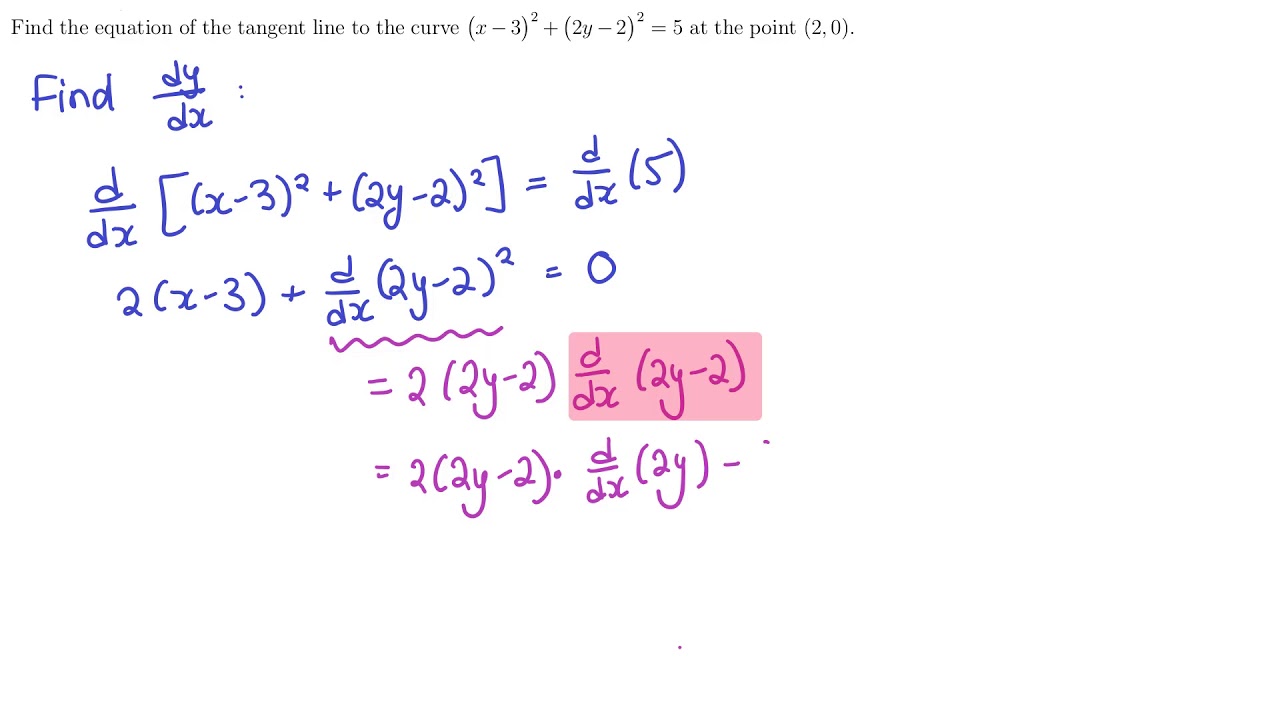



Implicit And Logarithmic Differentiation




Differentiate Each Function Y X 7 4 3 X 3 7x Chegg Com




Implicit Differentiation



1
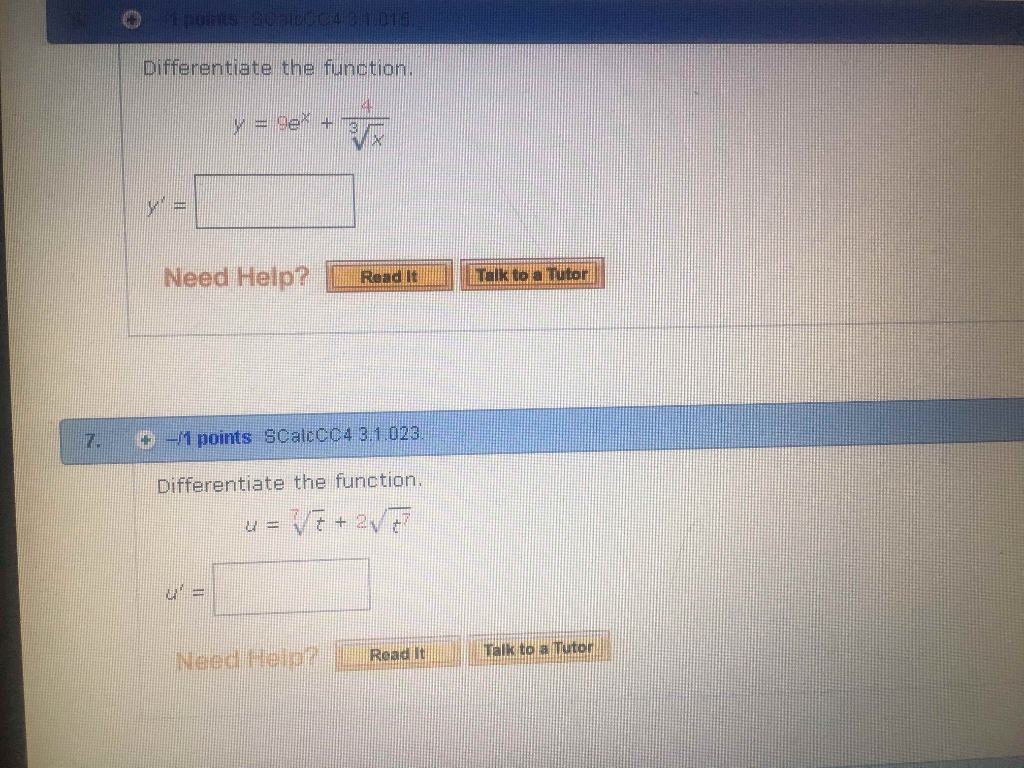



Differentiate The Function Y 9 E X 4 3 Chegg Com



5 Derivative Of The Logarithmic Function



What Is The Derivative Of The Absolute Value Of X Quora
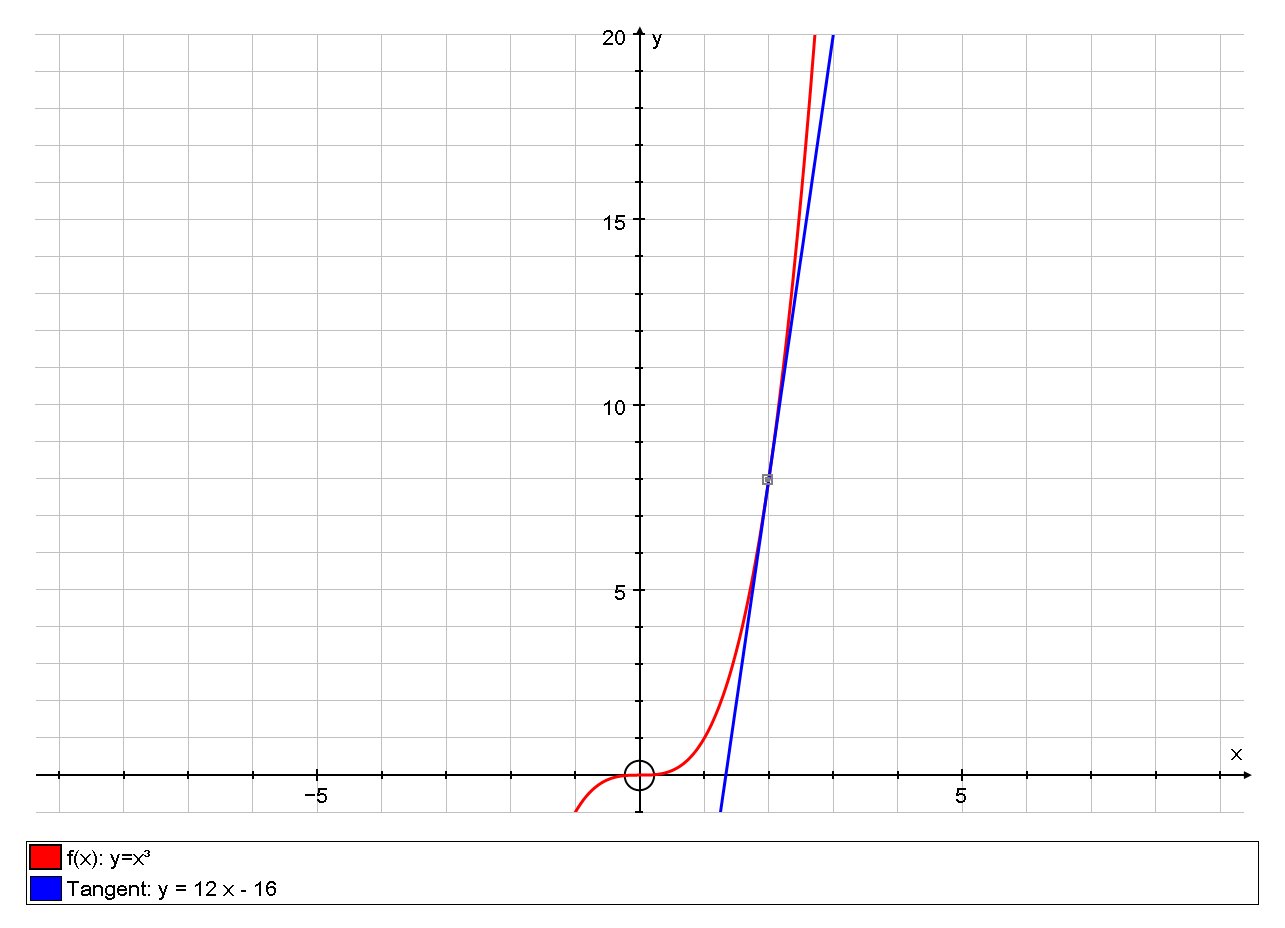



How Do You Find The Equation Of The Tangent Line To The Graph Of F X X 3 At Point 2 8 Socratic




The Second Derivative And Concavity




Implicit And Logarithmic Differentiation




Find The Directional Derivative Of The Function At Chegg Com



Www Usna Edu Users Oceano Raylee Sm223 Ch14 5 Stewart 16 Pdf



Definition Of The Derivative



How Do You Find The Equation Of The Line Tangent To The Graph Of Y Sin X At The Point X Pi Socratic



3 2 The Derivative As A Function Calculus Volume 1




3 Ways To Differentiate The Square Root Of X Wikihow



Q Tbn And9gct1yz L1jgg9fhlgbbf5vzrvs60eoq77tzx6sqadloeh I33ptd Usqp Cau




If Y X 2 2x 3x 4 Then Find Dy Dx



3 8 Implicit Differentiation Calculus Volume 1




Worked Example Differentiating Related Functions Video Khan Academy
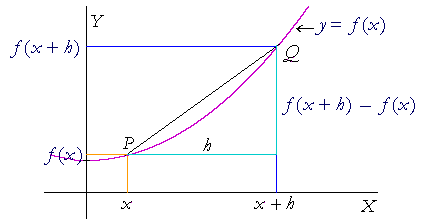



The Meaning Of The Derivative An Approach To Calculus




Implicit Differentiation




Solved Consider The Function Below A Differentiate Wit Chegg Com




Ex 6 2 8 Find X For Which Y X X 2 2 Is Increasing
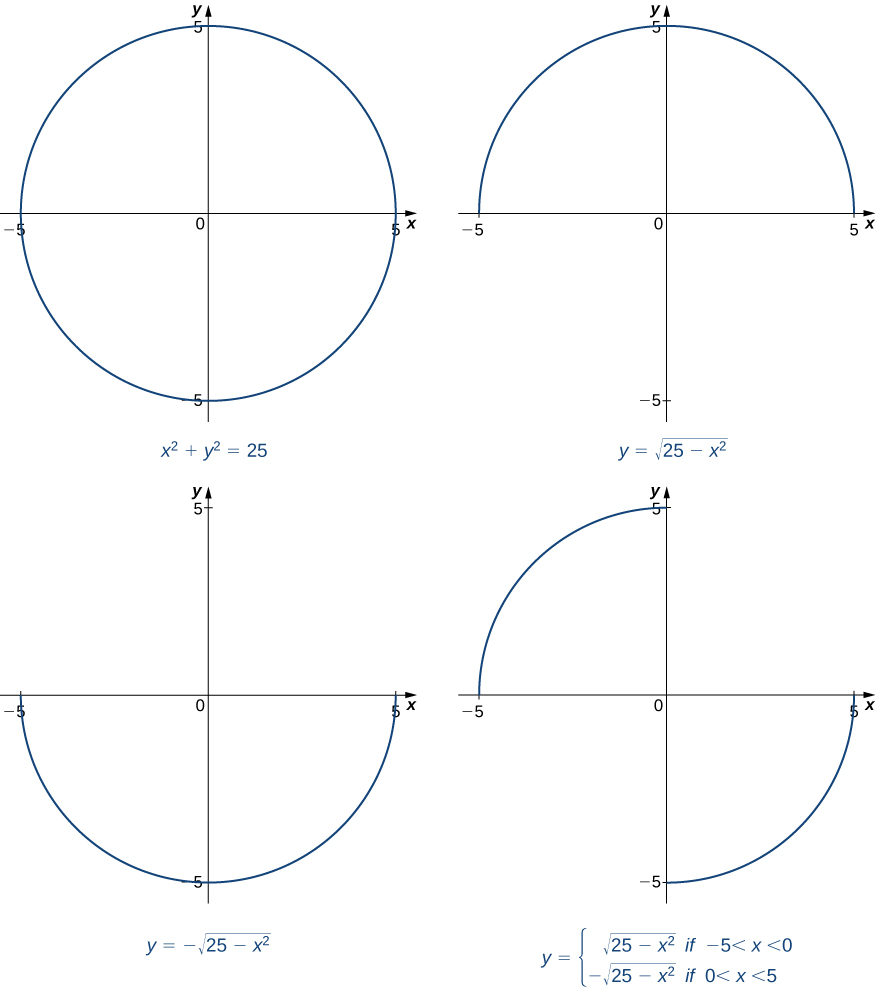



3 8 Implicit Differentiation Calculus Volume 1




Ex 5 5 7 Differentiate The Function Log X X X Log X
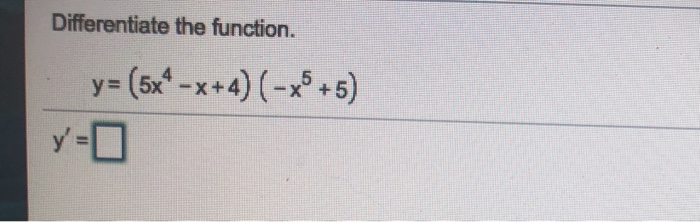



Solved Differentiate The Function Y 5x4 X 4 X5 5 Y 0 Chegg Com




Derivative Wikipedia



Curve Sketching




Differentiating Related Functions Intro Video Khan Academy



Implicit Differentiation




Ex 5 2 8 Differentiate Cos Root X With Respect To X




Differentiate Each Of The Following Functions 3x 2 Chegg Com




Differentiate The Function Y 6 In X Y Chegg Com




Worked Example Differentiating Related Functions Video Khan Academy




Finding A Derivative Using The Definition Of A Derivative Youtube




Find Dy Dx Y X 2 1 3 2x 1 Sqrt X 3 4x 1



1




Derivative Wikipedia



Slope Of A Curve At A Point Calculus Socratic



If X Y Y X What Is Dy Dx Quora



0 件のコメント:
コメントを投稿