Derivative x^2(xy)^2 = x^2y^2 Extended Keyboard;$\begingroup$ $\ln \sqrt{t} = \frac{1}{2}\ln t$ Hence we have $\frac{1}{2}\ln(x^2y^2) = \arctan(y/x)$ Bring the 2 to the right hand side $\endgroup$ – user Apr 21 '17 at 916 $\begingroup$ so we simplify it using logarithmic rules before proceed with derivatives?Find the gradient of f(x,y)=ln(x^2y^2) Expert Answer Who are the experts?

Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com
Partial derivative of ln(sqrt(x^2+y^2+z^2))
Partial derivative of ln(sqrt(x^2+y^2+z^2))-Derivative of ( (4x7)^5)/ ( (2x^23)^4) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving processSteps math\dfrac{d}{dx}\left(x^2e^x\sin \left(x\right)\right)/math Apply the power rule math\left(f\cdot g\right)'=f'\cdot gf\cdot g' f=x^2,\g=e^x\sin \left




Solving The Derivative Of Ln X Video Lesson Transcript Study Com
Explanation I am assuming by ln(x2 1)1 2 that you mean ln(√x2 1) rather than √ln(x2 1) By the chain rule, d dx f (g(x)) = f '(g(x))g'(x) or, dy dx = dy du du dx So d dx {ln(x2 1)1 2} = d dx {1 2ln(x2 1)} (by the power log rule) ∴ d dx {ln(x2 1)1 2} = 1 2 d dx {ln(x2 1)}The slope and ycoordinate at the given point are y = 3ln(24) = 178 y′(2) = 12 2 = 6 y = 3 ln ( 2 4) = 178 y ′ ( 2) = 12 2 = 6 Given the slope and the ycoordinate, the equationFree implicit derivative calculator implicit differentiation solver stepbystep This website uses cookies to ensure you get the best experience By using this
Using the derivative formula and the chain rule, f′ (x) = etan ( 2x) d dx(tan(2x)) = etan ( 2x) sec2(2x) ⋅ 2 Example Combining Differentiation Rules Find the derivative of y = ex2 x Solution Use the derivative of the natural$\endgroup$ – MMass Apr 21 '17 at 925Derivative Calculator Step 1 Enter the function you want to find the derivative of in the editor The Derivative Calculator supports solving first, second, fourth derivatives, as well as implicit differentiation and finding the zeros/roots You can also get a better visual and understanding of the function by using our graphing tool
The Second Derivative of ln(2x) To calculate the second derivative of a function, you just differentiate the first derivative From above, we found that the first derivative of ln(2x) = 1/x So to find the second derivative of ln(2x), we just need to differentiate 1/x If we differentiate 1/x we get an answer of (1/x 2)How do you place 02,This video illustrates the tangent line to the 3D surface to illustrate the meaning of the value of a directional derivativewebsite http//mathispower4ucom
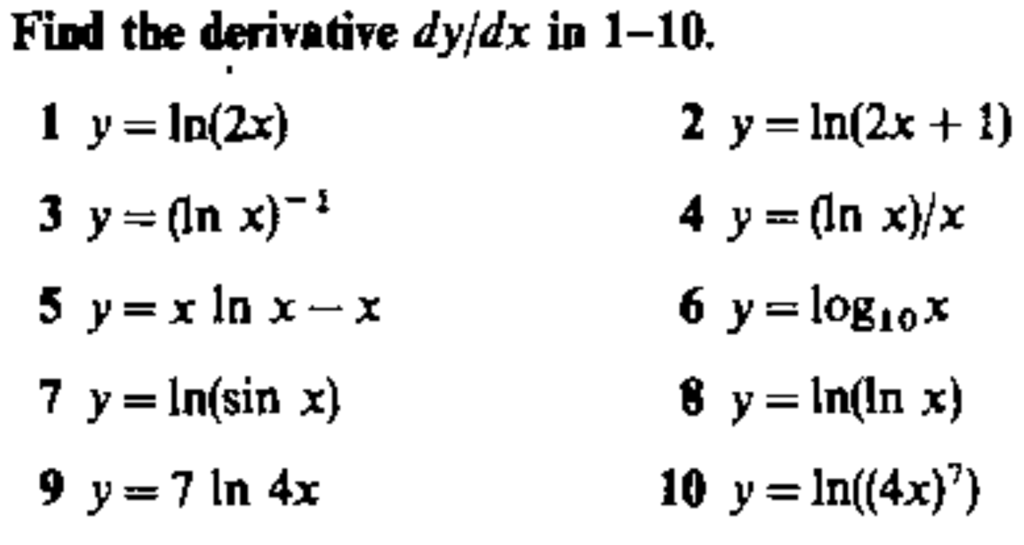



Find The Derivative Dyjdx In 1 10 1 Y Ln 2 X 3 Chegg Com
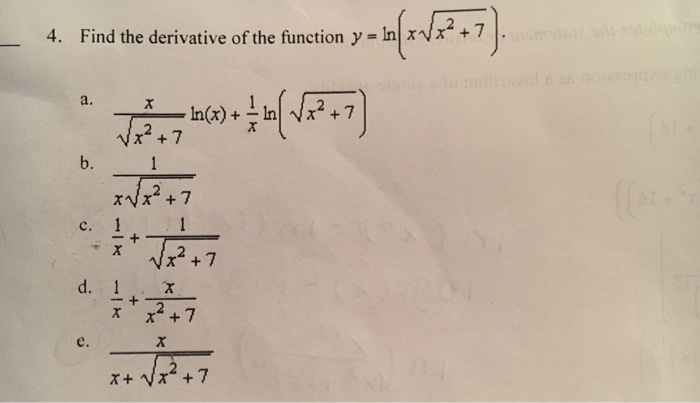



Find The Derivative Of The Function Y Ln X Chegg Com
Derivative of ln(x^2) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving processThe Derivative Calculator supports computing first, second, , fifth derivatives as well as differentiating functions with many variables (partial derivatives), implicit differentiation and calculating roots/zeros You can also check your answers!Interactive graphs/plots help visualize and better understand the functions



Implicit And Logarithmic Differentiation




What Is The Derivative Of Math E Ln X Math And How Did You Get There Quora
If we have f (x, y) = ln (x 2 y 2) Note that the y term is missing here, and using the chain rule with ln, we get d / d x (ln (x 2 y 2)) = x 2 y 2 1 d / d x (x 2 y 2) = x 2 y 2 1 (2 x 0) = x 2 y 2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicAnswer to What is the derivative of ln(x^2 y^2)?
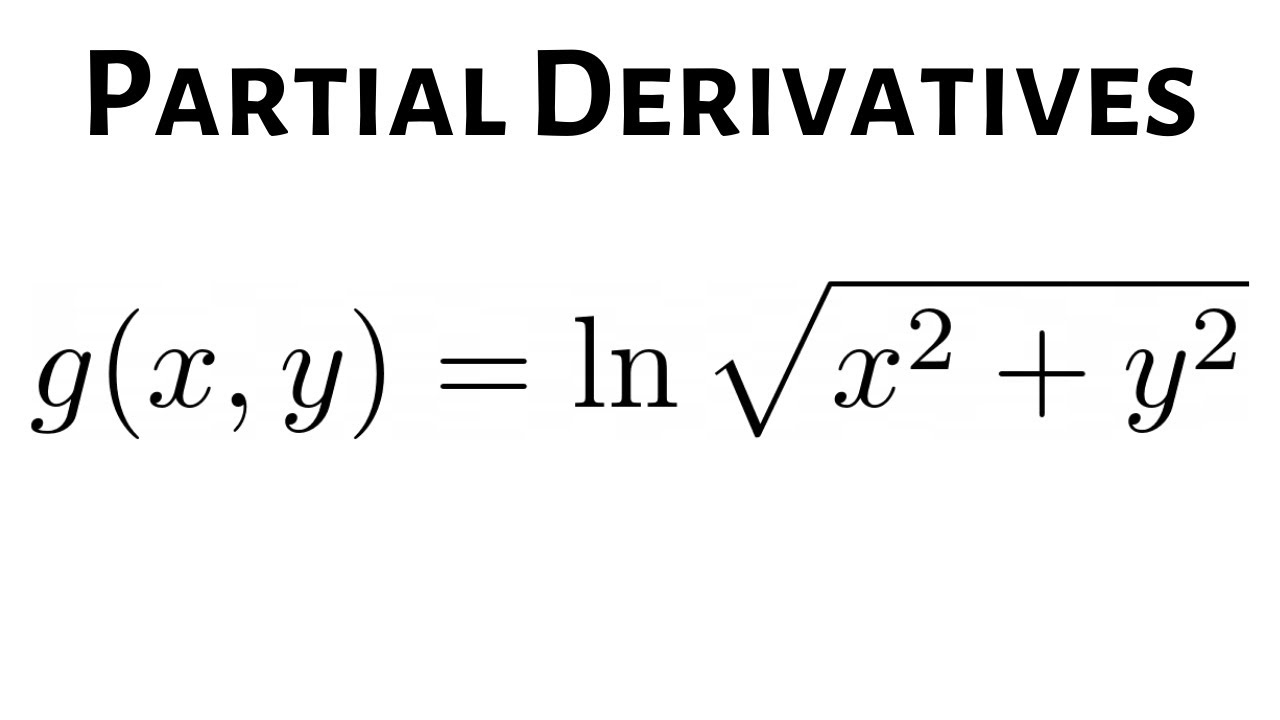



Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube



Derivative Of Natural Log Y Ln X Geogebra
Problem 45 Suppose the function f satisfies the conditions (i) f(x y) = f(x)f(y) for all the x and y (ii) f(x) = 1 xg(x) where limx → 0g(x) = 1 Show that the derivative f 4 Answers4 z ,which is worth noting in its own right for further use Another Chain rule approach is to use u = cosh − 1x y ↔ x = ycoshu Then x2 y2 = y2 y2cosh2u = y2sinh2u, so ln(x √x2 y2) = ln(ycoshu ysinhu) = ln(yeu) = u lny where we have recalled the definitions of hyperbolic sine and cosine So I feel we would get$$\frac{\partial}{\partial x} \ln(x^2y^2)=\frac{2x}{x^2y^2}$$ and with respect to $y$ $$\frac{\partial}{\partial y} \ln(x^2y^2)=\frac{2y}{x^2y^2}$$ Is that right?



Partial Derivative Ln X 2 Y 2



Find The Derivative Of The Function 5 Y Ln 2 Chegg Com
If we have f(x, y) = \ln(x^2 y^2) Note that the y term is missing here, and using the chain rule with \ln, we get d/dx ~(\ln(x^2 y^2)) = \dfrac{1}{x^2 y^2}~d/dx~ (x^2 y^2) = \dfrac{1}{x^2 y^2}(2x0) =\dfrac{2x}{x^2 y^2} About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsLearn how to solve implicit differentiation problems step by step online Find the implicit derivative (d/dx)(x^2(x^2y^2)=y^2) Apply implicit differentiation by taking the derivative of both sides of the equation with respect to the differentiation variable Apply the product rule for differentiation (f\cdot g)'=f'\cdot gf\cdot g', where f=x^2 and g=x^2y^2




Solving The Derivative Of Ln X Video Lesson Transcript Study Com




Derivative Of Ln X Natural Logarithm More
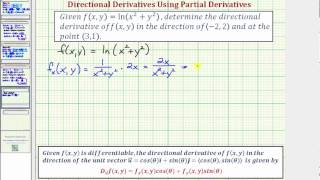
Find harmonic conjugate of u(x,y)=ln(x^2y^2) and specify the region it is defined then show u has no harm conj on C\{0} Homework Equations The Attempt at a Solution Ok so i found the harmonic conj by converting to polar and found it to be v(r,Θ) = Θ I am having trouble finding out where v is defined Also it seems our analytic function fCalculus Find the Derivative f (y) = square root of x^2y^2 f (y) = √x2 y2 f ( y) = x 2 y 2 Use n√ax = ax n a x n = a x n to rewrite √x2 y2 x 2 y 2 as (x2 y2)1 2 ( x 2 y 2) 1 2 d dx (x2 y2)1 2 d d x ( x 2 y 2) 1 2 Differentiate using the chain rule, which states that d dx f (g(x)) d d x f ( g ( x)) is f '(g(x))gDerivative of ln(x^2)5ln(y) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving process




How Do You Find The Derivatives Of Z Ln Y 4 1 2 Y 1 3 Socratic



Ex 3 Find A Value Of A Directional Derivative F X Y Ln X 2 Y 2 Youtube
//googl/JQ8NysFirst Order Partial Derivatives of f(x, y) = ln(x^4 y^4)Thus, the derivative of ln x2 is 2/x Note this result agrees with the plots of tangent lines for both positive and negative x For x = 2, the derivative is 2/2 = 1, which agrees with the plot And for x = 2, the derivative is 2/ (2) = 1, which agrees with the negative sloping tangent line at x = 2Derivative of ln(xsqrt(1x^2)), Full playlist https//wwwyoutubecom/playlist?list=PLj7p5OoL6vGzLwDjpT3gOA1K3RwUo8jDIf you enjoy my videos, then you can




Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com




What Is The Differentiation Of Y Ln X With Respect To X Where Represents Modulus Function Quora
Find the implicit derivative (d/dx) (x^2y^2=1) Apply implicit differentiation by taking the derivative of both sides of the equation with respect to the differentiation variable The derivative of the constant function (1) is equal to zero The derivative of a sum of two functions is the sum of the derivatives of each functionExperts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high 94% (17 ratings) When you take theFind the Derivative d/dx natural log of x^2y^2 ln (x2 y2) ln (x 2 y 2) Differentiate using the chain rule, which states that d dx f (g(x)) d d x f (g (x)) is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = ln(x) f (x) = ln (x) and g(x) = x2 y2 g (x) = x 2 y 2 Tap for more steps




Find The Derivatives Y Ln X 3 4 Y 2 X 3 1 Chegg Com
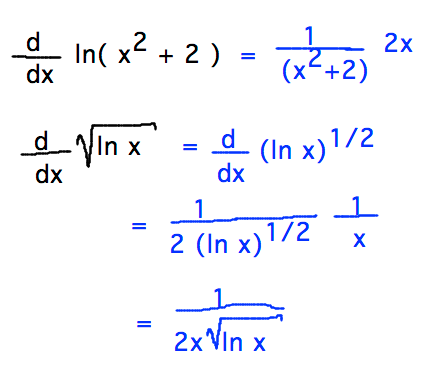



Geneseo Math 222 01 Functions
Larson Calculus 133 #28 First Partial Derivatives of g(x, y) = ln(sqrt(x^2 y^2))Please Subscribe here, thank you!!!//googl/JQ8NysDerivative of f(x) = ln(sqrt(2x))If y = xsqrt(1 x^2) then y^2 = x^2(1 x^2) = x^2 x^4 Now differentiate implicitly 2ydy = (2x 4x^3)dx, therefore, cancel 2s and x and make dy/dx the subject of the formula ydy = (x 2x^3)dx = x(1 2x^2)dx => dy/dx = x(1 2x^2)/y => dy/




Find The Derivative Of The Function Y Ln 4 Chegg Com



What Is The Differentiation Of Ln X And Log X Quora
1y=16(25)^x 2y=08(128)^x 3y=17(1/5)^x'' How do I determine if this equation is a linear function or a nonlinear function? How to find partial derivative $\frac{u}{\sqrt{x^2 y^2}} \arctan\frac{u}{\sqrt{x^2 y^2}} 1 = 0$ 4 Finding the limit by using the definition of derivative Derivative of y = ln u (where u is a function of x) Unfortunately, we can only use the logarithm laws to help us in a limited number of logarithm differentiation question types Most often, we need to find the derivative of a logarithm of some function of xFor example, we may need to find the derivative of y = 2 ln (3x 2 − 1) We need the following formula to solve such



Derivative 1 2 1 2 Ln X 1 X 1 Arctanx Mathskey Com




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange
By signing up, you'll get thousands of stepbystep solutions to your homework questions YouIf we have f (x, y) = \ln (x^2 y^2) Note that the y term is missing here, and using the chain rule with \ln, we get d/dx ~ (\ln (x^2 y^2)) = \dfrac {1} {x^2 y^2}~d/dx~ (x^2 y^2) = \dfrac {1} {x^2 y^2} (2x0) =\dfrac {2x} {x^2 y^2}Derivative of ln (x^2y) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving process




Implicit Differentiation Advanced Example Video Khan Academy




Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com
Derivative of y^2*e^ (2x) Derivative of y^2*e^ (2x) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving processTo justify your feeling, you can apply the chain rule to the maps g\colon x\mapsto x^2y^2 (where y is fixed) and f\colon x\mapsto \ln x It is correct To justify your feeling, you can apply the chain rule to the maps g x ↦ x 2 y 2 (where y is fixed) and f x ↦ ln xPlease Subscribe here, thank you!!!



Second Derivative Of Ln X Sqrt 1 X 2 Youtube




Solving The Derivative Of Ln X Video Lesson Transcript Study Com
Answer to Find the partial derivative of the function u=ln (x^2y^2z^2) By signing up, you'll get thousands of stepbystep solutions to yourIf we have f(x, y) = \ln(x^2 y^2) Note that the y term is missing here, and using the chain rule with \ln, we get d/dx ~(\ln(x^2 y^2)) = \dfrac{1}{x^2 y^2}~d/dx~ (x^2 y^2) = \dfrac{1}{x^2 y^2}(2x0) =\dfrac{2x}{x^2 y^2}Please Subscribe here, thank you!!!




The Derivative Of Lnx And Examples Mathbootcamps




Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com
2 x is a function of y 3 x and y are both functions of some variable (call it t) 4 x is a constant 5 y is a constant Setup Assuming y is a function of x 2 Assuming x is a function of y It's just the same steps as number 1, but with y and x replaced, sincePartial derivative of ln (sqrt (x^2y^2)x) full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \geDerivative of ln(x*sqrt(x^2)), derivative of ln(xsqrt(x^21)), If you enjoy my videos, then you can click here to subscribe https//wwwyoutubecom/blackpe




Lesson 16 Derivatives Of Logarithmic And Exponential Functions



3




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange



What Is The Nth Derivative Of Logx Quora



Implicit And Logarithmic Differentiation




Find The Derivative Of Y Lnx X 2 3x 1




What Is The Equation Of The Tangent Line Of F X Ln X 3 X 7x At X 3 Socratic




Review 7 2 Find The Derivative 1 F X Ln 3x 4 X F X Ln 1 X 1 X2 2 1 X3 3 Ln 1 X Ln 1 X 2 2 Ln 1 X Ppt Download




Proof The Derivative Of F X Ln X D Dx Ln X 1 X Implicit Diff Youtube
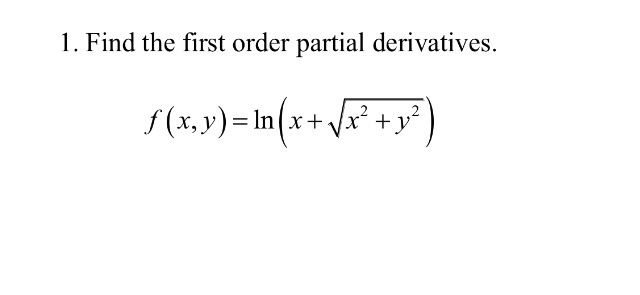



Find The First Order Partial Derivatives F X Y Chegg Com




Derivative Of Ln X Natural Logarithm More




Functions Of Several Variables Copyright C Cengage Learning All Rights Reserved Ppt Download




Implicit And Logarithmic Differentiation




Ex 3 Find A Value Of A Directional Derivative F X Y Ln X 2 Y 2 Youtube
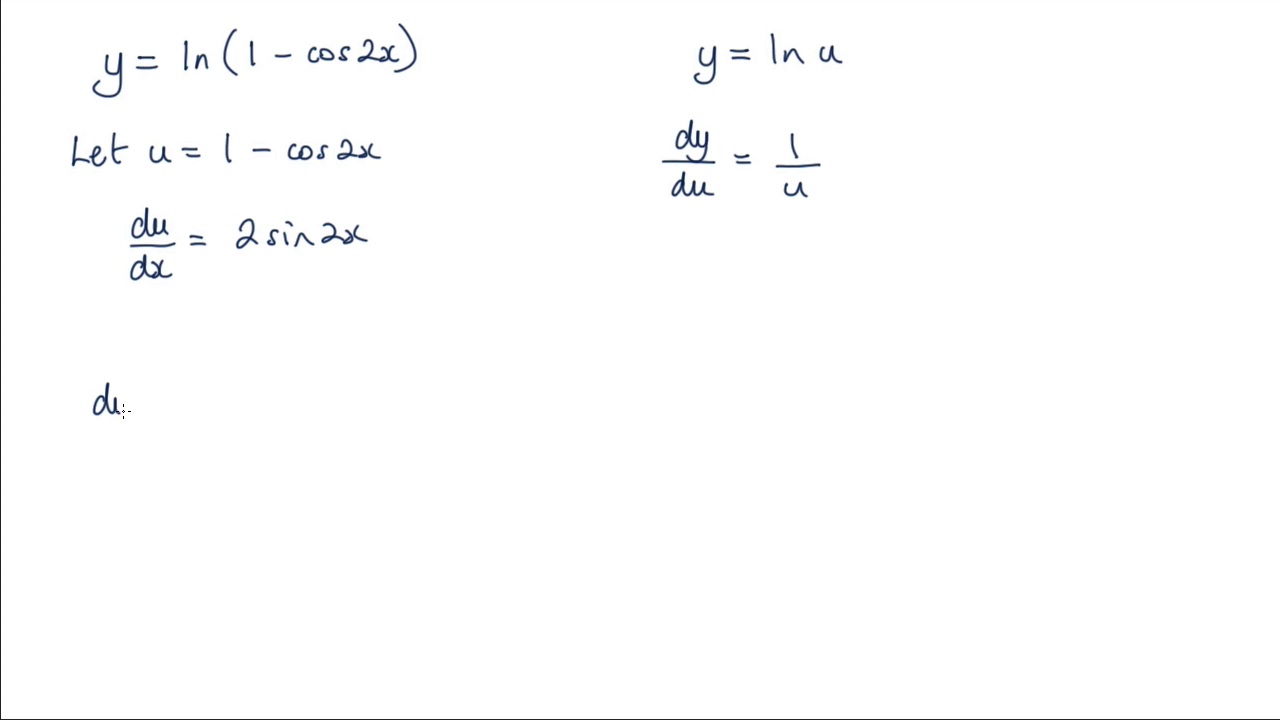



How To Differentiate Ln 1 Cos2x Using The Chain Rule Youtube
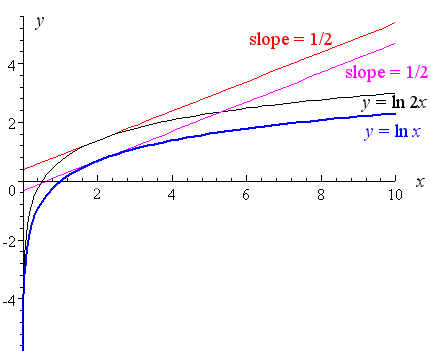



5 Derivative Of The Logarithmic Function




5 Derivative Of The Logarithmic Function




Find Derivative Of Y E Sqrt Sin Ln X 2 7 5




Derivative Of The Logarithmic Function Y Ln Xsqrt X 2 2 Using Proper Logarithmic Functions Math Videos Math
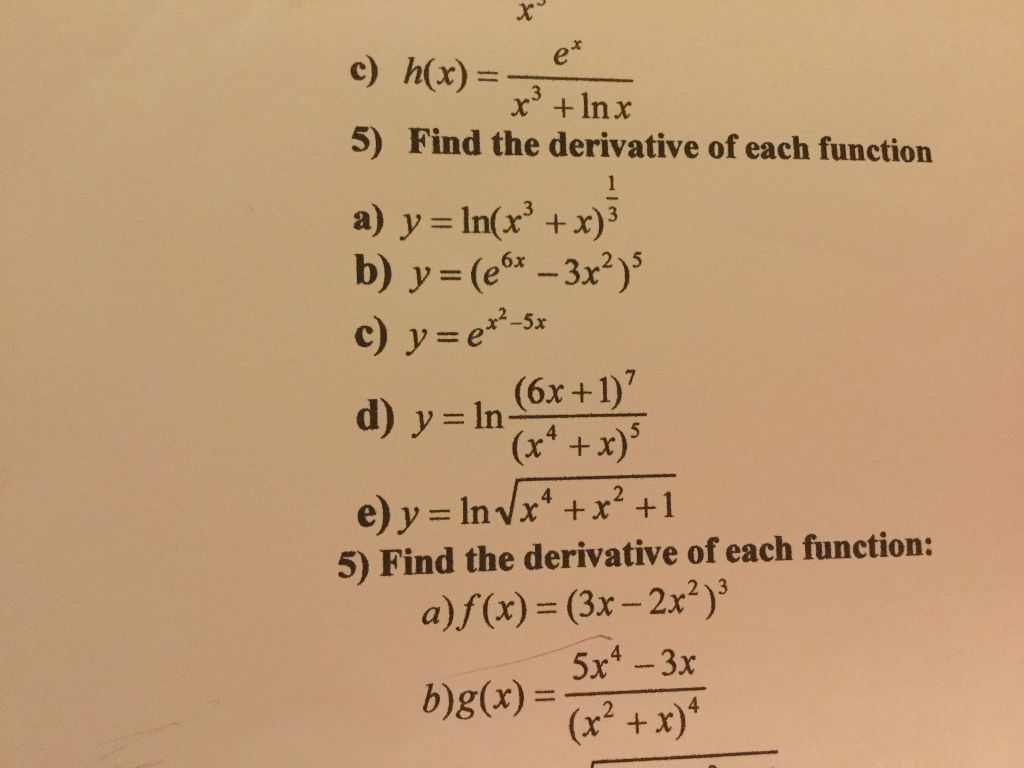



Find The Derivative Of Each Function Y Ln X 3 Chegg Com




Calculus Natural Log Derivatives Ln 2x 1 3 Sqrt X 2 1 Youtube




Derivative Of Ln X Video Khan Academy




Solving The Derivative Of Ln X Video Lesson Transcript Study Com



Ex 3 Find A Value Of A Directional Derivative F X Y Ln X 2 Y 2 Math Help From Arithmetic Through Calculus And Beyond




Int Ln X 1 X 1 X 2 1 Dx Is Equal To A 1




Partial Differentiation And Multiple Integrals Pdf Free Download




Calculus 1 Ch 5 1 Derivative Of E X And Lnx 12 Of 24 Other Natural Log Derivatives Youtube
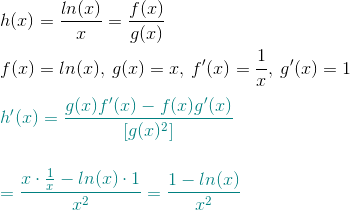



Finding The Derivative Of Ln X X How To Steps Study Com




Implicit Derivation Of Logarithmic Function Y Ln X 2 Y 2 Youtube



5 Derivative Of The Logarithmic Function




Calculus Derivative Of The Natural Log Ln Video Lessons Examples Solutions



Find The First Order Partial Derivatives Z Ln X Chegg Com



Larson Calculus 5 1 50 Differentiate Ln Sqrt X 2 4 Youtube
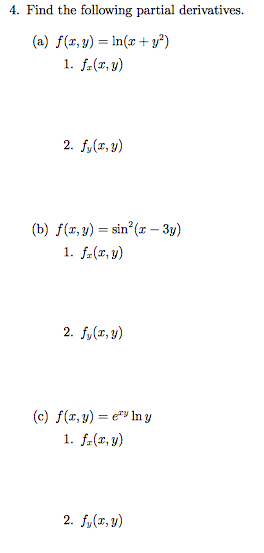



4 Find The Following Partial Derivatives A Chegg Com
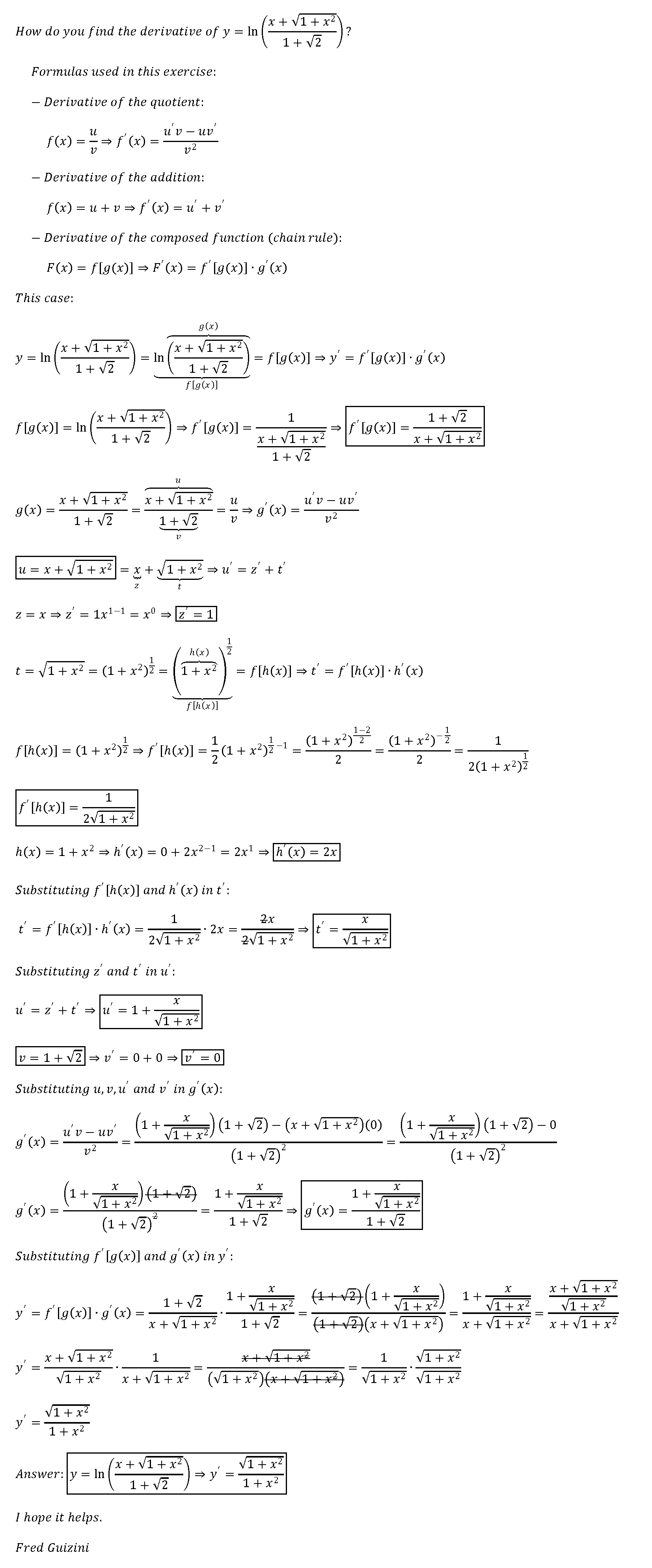



How Do You Find The Derivative Of Y Ln X Sqrt 1 X 2 1 Sqrt2 Socratic




Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com




How To Differentiate Y Ln Lnx Using The Chain Rule Youtube




Derivatives Days Ppt Download




Let Y Ln X 2 Y 2 Determine The Derivative Y At Chegg Com




Derivative Of Ln X 2 Y 2 Novocom Top
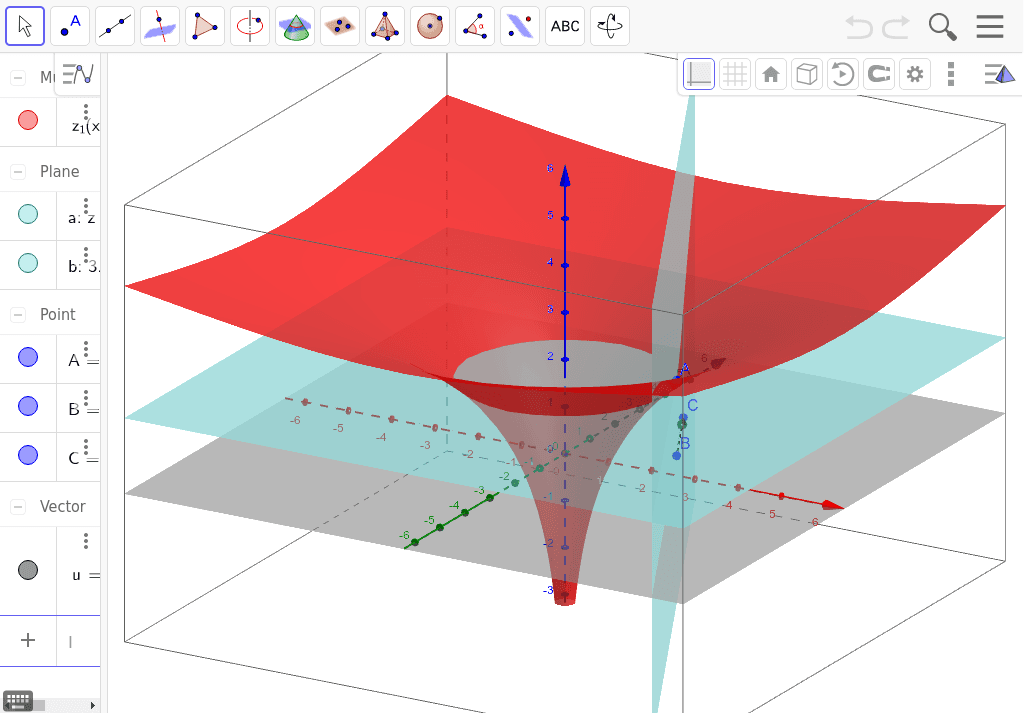



Ln X 2 Y 2 With Directional Derivative Geogebra




Logarithmic Derivatives Y Ln X 8 1 3 2 Youtube




Ppt Section 3 5 Find The Derivative Of G X X 2 Ln X You Will Need To Use The Product Rule Powerpoint Presentation Id




Derivative Calculator Wolfram Alpha
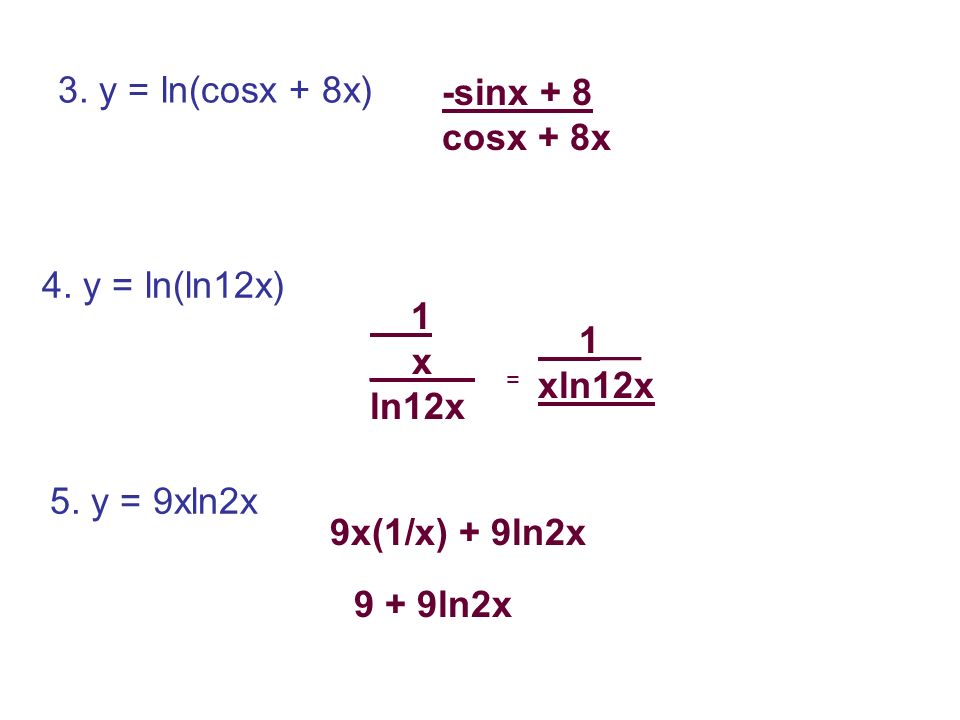



Review 7 2 Find The Derivative 1 F X Ln 3x 4 X F X Ln 1 X 1 X2 2 1 X3 3 Ln 1 X Ln 1 X 2 2 Ln 1 X Ppt Download




Differentiate Y Ln X 3 Youtube



Search Q Integral Of Ln X Tbm Isch




Solving The Derivative Of Ln Sqrt X Video Lesson Transcript Study Com



How Do You Determine Whether The Function F X Ln X 2 7 Is Concave Up Or Concave Down And Its Intervals Socratic




Find Y For Ln X Y Arctan Xy Mathematics Stack Exchange




Find The Indicated Second Order Partial Derivatives Chegg Com
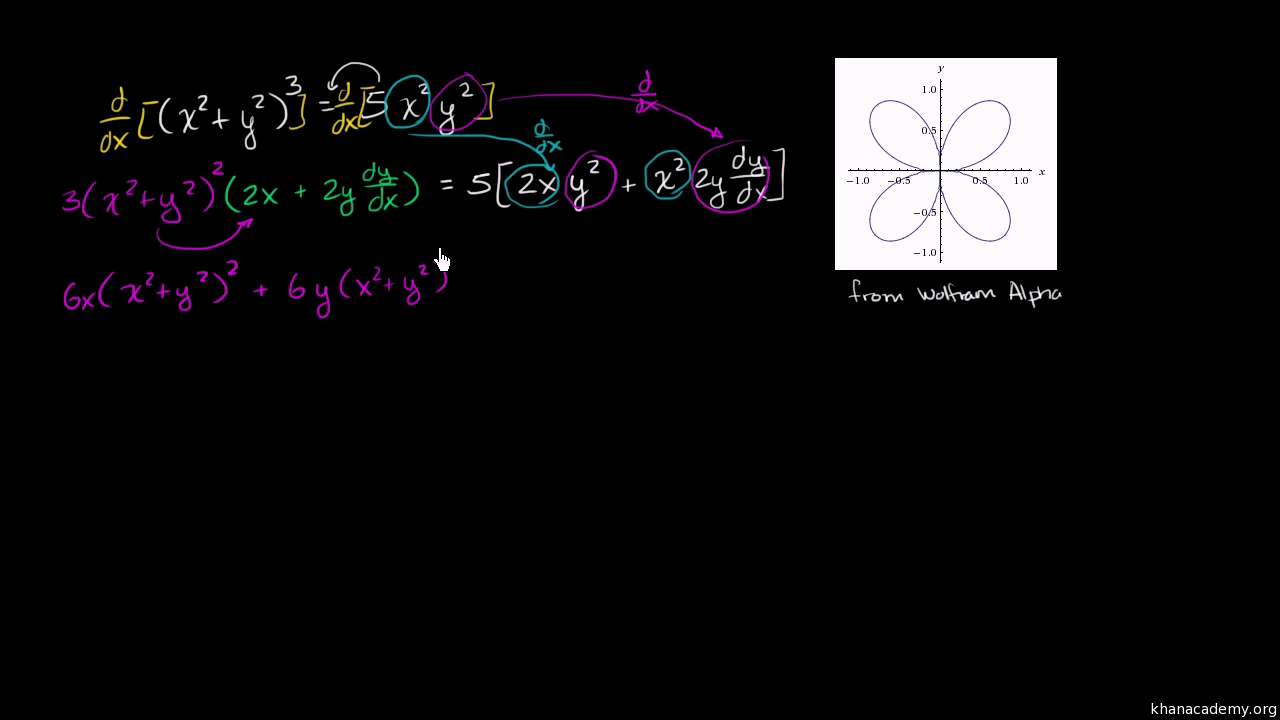



Implicit Differentiation Advanced Example Video Khan Academy




At0wbebfqjhzjm



How To Differentiate Ln X 2 Using The Chain Rule Youtube



Solved Lety Ln X 2 Y 2 Y Ln X2 Y2 Determine The Derivativey Yat The Point E 7 49 7 E749 7 Course Hero




The Derivative Of Lnx And Examples Mathbootcamps




Proof The Derivative Of Ln X Is 1 X Video Khan Academy




Calculate The Second Order Partial Derivatives F X Chegg Com
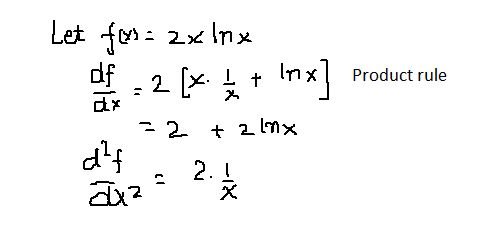



How Do You Find The First And Second Derivative Of 2x Ln X Socratic




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange



Derivative Calculator With Steps



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau



What Is The Differentiation Of Ln Sinx Quora




Answered 54 Y Ln X Cos Cos X 3d Bartleby



Find The Derivative Of Y With Respect To X Y Ln Chegg Com
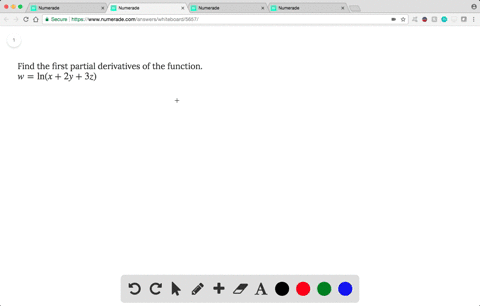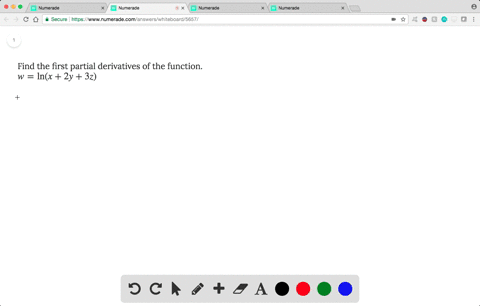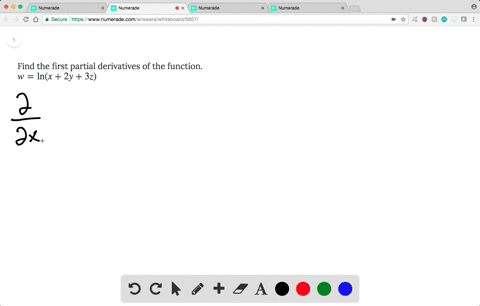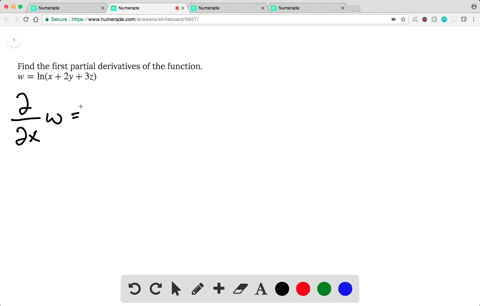



Solved Find The First Partial Derivatives Of The




How Do You Find The First And Second Derivative Of Ln X X 2 1 1 2 Socratic



Could You Differentiate Sin Y Ln X X 2sin Y Wrt X And Explain Why The Derivative Of 2sin Y Becomes 0 Quora
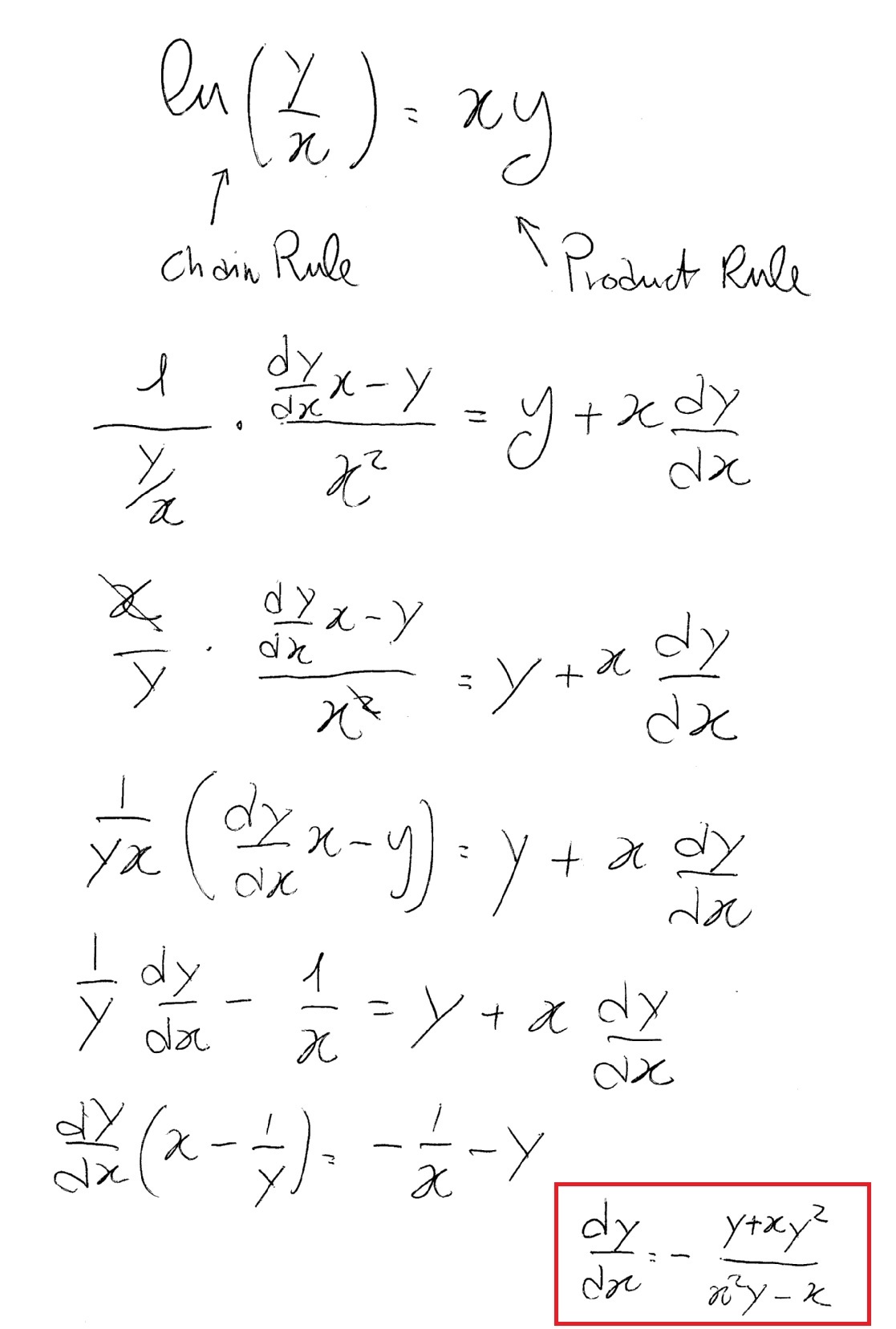



How Do You Differentiate Ln Y X Xy Socratic




Help Please For 1 2 6 Find The First Order Partial Chegg Com




Derivative Of Ln X Video Khan Academy




First Order Partial Derivatives Of F X Y Ln X 4 Y 4 Youtube
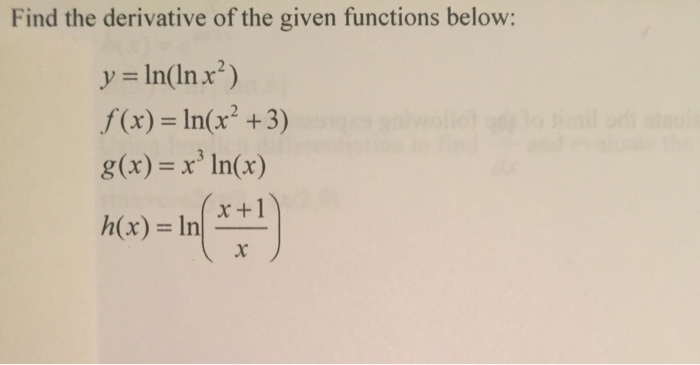



Find The Derivative Of The Given Functions Below Y Chegg Com
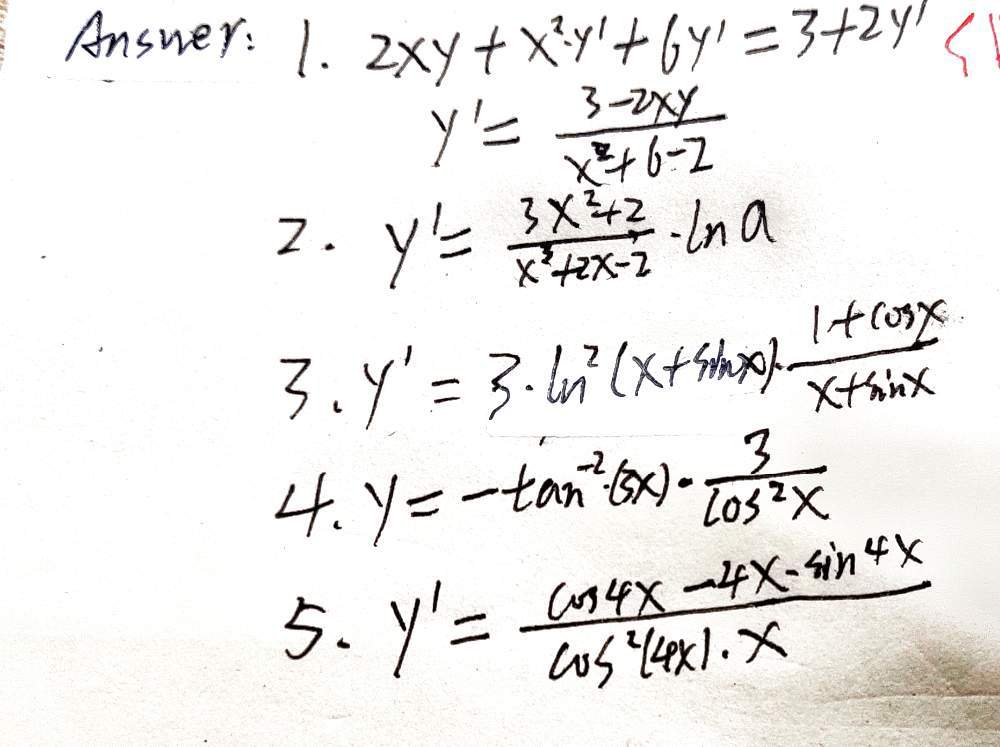



Learning Task 1 Determine The Derivative Of The F Gauthmath



5 Derivative Of The Logarithmic Function




Y Ln X 2 Derivative



Q Tbn And9gcq9arl5ab K Kkztqdma6czzlslnfprp6ljv7o6a18 5qqda4yy Usqp Cau




Implicit Derivation Of Logarithmic Function Y Ln X 2 Y 2 Youtube



0 件のコメント:
コメントを投稿